How and why does this work ?
tant = sint/cost
but also
tanp = cost + sint / cost - sint
p = t + pi/4
basically, think of it as rotating the entire frame by pi/4 and then doing stuff on this plane as we usually do with unit circle trigonometry. BUT, in this new plane, still calculating things wrt old frame (t co-ordinates), and doing that gives us cost + sint / cost - sint.
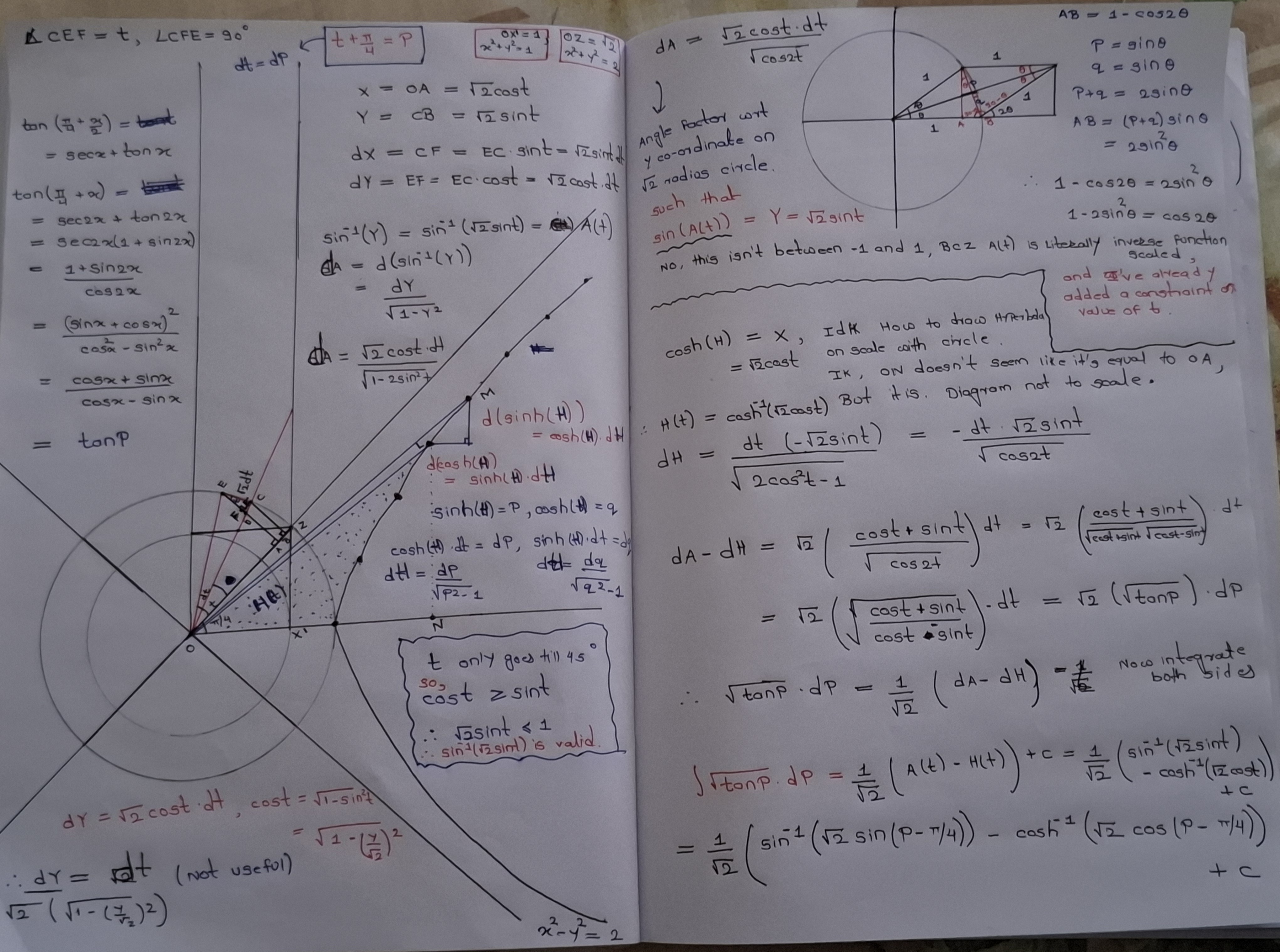
cost + sint and cost - sint both have range -√2 to √2. i.e. they parameterize the circle u^2 + v^2 = 2,
cost + sint = √2 sin(t + pi/4) = √2sinp = u
cost - sint = √2 cos(t + pi/4) = √2cosp = v
Suppose, we only restrict our original domain t to -pi/4 to pi/4. why this ?? because this is enough to make them go around the first quarter.
cost + sint = √2sint(t + pi/4) , suppose we start from angle -pi/4 and move till angle 0, that'd make our point move from 0 to 1. and as we move further pi/4 from 0, then we move from 1 to √2. But this is same as moving on circle of radius √2 angle 0 to pi/2.
A(t) = arcsin(Y) = arcsin(√2sint) = valid if t goes from 0 to 45.
Y = sin(A(t)) = √2sint = Duality between same lengths before t <= 45 degrees between unit circle and √2 radius circle
dY = cos(A(t))dA(t) = sqrt(1 - sin^2(A(t)))dA(t) = sqrt(1 - 2sin^2t)dA(t)
But you know what, dY = √2costdt. because they're literally same lengths, it's just that above we defined things on unit circle by defining a variable A.
Here, it's the same length but on √2 radius circle. Think of it like matching vertical co-ordinates on unit circle and √2 radius circle. Argument — √2sint height is achieved on both of them at angle A(t) and t respectively. If we take increments on angles on both of them such that the fact that we get the same height on their respective circles, then there must be also equal increment/decrease in the height.

i.e. cos(A(t))dt = √2costdt
√2costdt = dA(t) * sqrt(1 - 2sin^2t)
dA(t) = √2costdt/sqrt(1-2sin^2t) = √2costdt/sqrt(cos2t)
what if we try to do the same with cos ?
H(t) = arccos(X) = arccos(√2cost) = not valid if t goes from 0 to 45.
X = cos(H(t)) = √2cost, simply not possible if t goes from 0 to 45.
√2cost goes from √2 to 1 in this domain. we want cos(H(t)) to do the same.
But cos(H(t)) will not do that, until we allow H(t) to be imaginary.
cos(iH(t)) = √2cost, it's possible, there exists some H(t) for which this is always true.
cos(iH(t)) = cosh(H(t))
So, actually
X = cos(iH(t)) = √2cost

dX = -idH(t)sin(iH(t)

dX = -idH(t)sqrt(1 - cos^2t = -√2sintdt (obviously)

dH(t) = -i√2sintdt/sqrt(1 - 2cos^2t) = -√2sintdt/sqrt(2cos^2t - 1)
dH(t) = -√2sintdt/sqrt(cos2t)
this is actually nice, because, even if now t is between 0 to 45, both numerator and denominator stays within trig rules.
dA = √2costdt/√cos2t

dH = -√2sintdt/√cos2t
dA = differential of angle that provided a direct path between y co-ordinates on the unit circle and the √2 radius circle.
dH = differential of angle that provided a direct path between x co-ordinates on the imaginary unit circle (unit hyperbola) and the √2 radius circle.
It's like a one complete angle with real and imaginary part (ofc not equal, why'd they be equal lol) the real part provides a way to reach the y co-ordinate from 0 to 1. And imagianary part provides a way to reach the x co-ordinate from 1 to √2.
Thus, the total angle associated with this process of full unwrapping of co-ordinates under given constraints becomes real part +/- imaginary part. This is an angle and it contains the full information to see the original full co-ordinates in one go. And even get the exact angle it is making in order to stay on the unit circle. and even predict future values.
dA + dH or dA - dH.

and the fact that you get this equal to sqrt(2tanp) dp, p = 45 + t, is kinda flex literally. Idk why this is coming to my mind,
If we have 2 sqrt(tanp)dp lengths, perp to each other, making 45 degree angle, then it's hypotenuse would be √2tanpdp. tanpdp is the length of the actual tangent to the circle of radius √2. Let's call the sqrt(tanp)dp as sqrt(circular effect). So when we did this pythagoras thing with taking it's equal incremental lengths in both directions, we got tanpdp. It's literally a simple circular effect for the √2 radius circle bro.
There are 2 mistakes/typos in this proof —
1) the hyperbola that i drew should be x^2 - y^2 = 1, not x^2 - y^2 = 2. Because i parameterized it with cosh(H) and sinh(H). But that doesn't change anything. All the ideas remains same.
2) On the first page top right side, i wrote d(cosx) = sinxdx. It should be -sinxdx. But again, I have never used this anywhere later in the proof, so doesn't make any difference.